Hay disponible una gran variedad de compuertas estándar, cada una con un comportamiento perfectamente definido, y es posible combinarlas entre si para obtener funciones nuevas. Desde el punto de vista practico, podemos considerar a cada compuerta como una caja negra, en la que se introducen valores digitales en sus entradas, y el valor del resultado aparece en la salida.
Cada compuerta tiene asociada una tabla de verdad, que expresa en forma de lista el estado de su salida para cada combinación posible de estados en la(s) entrada(s).
En la actualidad, una compuerta es un conjunto de transistores dentro de un circuito integrado, que puede contener cientos de ellas. De hecho, un microprocesador no es más que un chip compuesto por millones de compuertas lógicas.
Posiblemente la manera más sencilla de implementar funciones lógicas sea
mediante el uso de diodos, los cuales permiten el paso de la corriente
eléctrica en una sola dirección más no en la dirección contraria. Esta
manera de construir funciones lógicas es conocida de varias maneras
tales como "Diode Logic", "Diode-Diode Logic" o inclusive como
"Diode-Resistor Logic".
En el siguiente diagrama esquemático tenemos la función OR implementada con diodos:
El funcionamiento de este circuito es extremadamente sencillo. Si las entradas a los diodos
D1 y
D2 en las terminales 3 y 4 son "
0"
(cero voltaje aplicado en ellas) entonces no llegará voltaje alguno a
la terminal 1. En pocas palabras, cuando ambas entradas son "
0" la salida será "
0". Si aplicamos un voltaje (un "
1") a la terminal 3 y mantenemos la entrada a la terminal 4 en "
0", entonces la corriente eléctrica podrá fluir directamente de la terminal 3 a la terminal 1 poniendo un "
1" (el voltaje aplicado en la entrada del diodo
D1) en la salida. Esta corriente eléctrica no puede fluir por el diodo
D2 aunque su entrada sea "
0"
porque el diodo solo es capaz de conducir corriente eléctrica en la
dirección indicada por la flecha en su símbolo. Con esto, si la entrada
en la terminal 3 es "
1" y la entrada en la terminal 4 es "
0", la salida será "
1". Y lo mismo ocurrirá cuando la entrada en la terminal 3 sea "
0" y la entrada en la terminal 4 sea "
1". En pocas palabras, cuando cualquiera de las entradas es "
1" la salida será también "
1". Y si ambas entradas son "
1" la salida será "
1". Esta es precisamente la acción de un OR.
En el siguiente diagrama esquemático tenemos la función AND implementada con diodos:
Este circuito también tiene una explicación sencilla.
Si las entradas a los diodos
D1 y
D2 en las terminales 4 y 5 son "
1",
entonces al estar ambos lados de cada diodo al mismo potencial
eléctrico ninguno de ellos conducirá corriente eléctrica alguna (la
corriente eléctrica sólo puede fluir de un "
1" a un "
0") y la terminal 1 se mantendrá al mismo nivel del voltaje al cual está conectada a través de la resistencia
R1. En pocas palabras, cuando ambas entradas son "
1" la salida será "
1". Si aplicamos un "
0" a la terminal 4 y mantenemos la entrada a la terminal 5 en "
1", entonces la corriente eléctrica podrá fluir directamente a través del diodo
D1 de la fuente de voltaje a la terminal 4 siguiendo la flecha simbólica del diodo
D1, con lo cual el voltaje en la terminal 1 se desplomará al nivel de "tierra eléctrica", o sea a "
0". Con esto, si la entrada en la terminal 4 es "
0" y la entrada en la terminal 5 es "
1", la salida será "
0". Y lo mismo ocurrirá cuando la entrada en la terminal 4 sea "
1" y la entrada en la terminal 5 sea "
0". En pocas palabras, cuando una de las entradas es "
0" la salida será "
0". Y si ambas entradas son "
0" la salida será "
0". Esta es precisamente la acción de un AND.
La principal desventaja de utilizar únicamente diodos para implementar
funciones lógicas es que no hay manera alguna de implementar la función
NOT, los diodos no proporcionan manera alguna de poder invertir un "
1" lógico convirtiéndolo en un "
0",
o viceversa. Por otro lado, como los diodos no proporcionan
amplificación alguna (en el sentido eléctrico) de la potencia de la
señal digital, la señal se va deteriorando rápidamente por las pérdidas acumulativas de voltaje a través de los diodos.
Fue precisamente la invención del transistor bipolar lo que abrió el
camino para la miniaturización electrónica y la dramática reducción de
costos que permitieron la construcción de circuitos lógicos cada vez más
complejos a precios accesibles al consumidor general. En su esencia más
básica el transistor, además de su capacidad para poder amplificar
señales
analógicas tales como
señales de audio y video cuyos voltajes pueden tomar cualquier valor
dentro de ciertos rangos, tenía inherentemente la capacidad para poder
actuar como un
inversor lógico, esto es,
como un bloque NOT:
En este diagrama esquemático, podemos ver que si aplicamos un voltaje
Vin
de +5 volts a la base del transistor, el transistor se "encenderá"
conduciendo corriente eléctrica, y al hacer tal cosa el transistor se
comportará como un "corto circuito" con lo cual el voltaje
Vout
entre sus otras dos terminales, el colector (la terminal superior) y el
emisor (la terminal inferior) será prácticamente de cero. Si el
interruptor eléctrico a la izquierda del circuito es bajado de modo tal
que a la base del transistor ya no le llegue ningún voltaje, entonces el
transistor se comportará como un circuito "abierto", y el voltaje de
salida
Vout será el mismo que hay entre su colector y su emisor, o sea +5 volts. Si designamos al voltaje de +5 volts como un "
1" lógico y al voltaje de cero volts como un "
0" lógico, lo que tenemos en esencia es un circuito que con un "
1" a la entrada nos produce un "
0" a la salida, y con un "
0" a la entrada nos produce un "
1"
a la salida. Esta es precisamente la acción de un inversor NOT. Con la
adición de algunos cuantos componentes adicionales, podemos irle
agregando al transistor básico más terminales de entrada con las cuales
podemos construir otros bloques lógicos, además de proporcionarle al
diseño básico un funcionamiento eléctrico más estable que el que puede
proporcionar el circuito anterior.
COMPUERTA IF (Buffer)
La puerta lógica IF, llamada SI en castellano, realiza la función booleana de la igualdad. En los esquemas de un circuito electrónico se simboliza mediante un triangulo, cuya base corresponde a la entrada, y el vértice opuesto la salida. Su tabla de verdad es también sencilla: la salida toma siempre el valor de la entrada.
Esto significa que si en su entrada hay un nivel de tensión alto, también lo habrá en su salida; y si la entrada se encuentra en nivel bajo, su salida también estará en ese estado
En electrónica, generalmente se utilizan compuertas IF como amplificadores de corriente (buffers en ingles), para permitir manejar dispositivos que tienen consumos de corriente elevados desde otros que solo pueden entregar corrientes más débiles.
ENTRADA A SALIDA X
0 0
1 1
COMPUERTA NOT (Negación)
Esta
compuerta presenta en su salida un valor que es el opuesto del que esta
presente en su única entrada. En efecto, su función es la negación, y
comparte con la compuerta IF la característica de tener solo una
entrada. Se utiliza cuando es necesario tener disponible un valor lógico
opuesto a uno dado.
Se
simboliza en un esquema eléctrico en el mismo símbolo que la compuerta
IF, con un pequeño circulo agregado en su salida, que representa la
negación.
ENTRADA A SALIDA X
0 1
1 0
COMPUERTA AND (Y)
Con
dos o más entradas, esta compuerta realiza la función booleana de la
multiplicación. Su salida será un “1” cuando todas sus entradas también
estén en nivel alto. En cualquier otro caso, la salida será un “0”. El
operador AND se lo asocia a la multiplicación, de la misma forma que al
operador SI se lo asociaba a la igualdad.
En
efecto, el resultado de multiplicar entre si diferentes valores
binarios solo dará como resultado “1” cuando todos ellos también sean 1,
como se puede ver en su tabla de verdad. Matemáticamente se lo
simboliza con el signo “x”.
Podemos pensar en esta compuerta como una lámpara, que hace las veces de salida, en serie con la fuente de alimentación y dos o mas interruptores, cada uno oficiando de entrada. La lámpara se encenderá únicamente cuando todos los interruptores estén cerrados. En este ejemplo, el estado de los interruptores es “1” cuando están cerrados y 0 cuando están abiertos. La salida esta en 1 cuando la
lámpara esta encendida, y en 0 cuando esta apagada.
ENTRADA A ENTRADA B SALIDA X
0 0 0
0 1 0
1 0 0
1 1 1
COMPUERTA OR (O)
La
función booleana que realiza la compuerta OR es la asociada a la suma, y
matemáticamente la expresamos como “+”. Esta compuerta presenta un
estado alto en su salida cuando al menos una de sus entradas también
esta en estado alto.
En cualquier otro caso, la salida será 0. Tal como ocurre con las compuertas AND, el número de entradas puede ser mayor a dos.
Un circuito eléctrico equivalente a esta compuerta esta compuesto por una lámpara conectada en serie con la alimentación y con dos o mas interruptores que a su vez están conectados en paralelo entre si.
Nuevamente, los interruptores serian las entradas, y la lámpara la salida. Si seguimos las convenciones fijadas en el ejemplo visto al explicar la compuerta AND, tenemos que si ambos interruptores están abiertos (o en 0), la lámpara permanece apagada. Pero basta que cerremos uno o más de los interruptores para que la lámpara se encienda.
ENTRADA A ENTRADA B SALIDA X
0 0 0
0 1 1
1 0 1
1 1 1
COMPUERTA NAND (NO Y)
Cualquier compuerta lógica se puede negar, esto es, invertir el estado de su salida, simplemente agregando una compuerta NOT que realice esa tarea. Debido a que es una situación muy común, se fabrican compuertas que ya están negadas internamente. Este es el caso de la compuerta NAND: es simplemente la negación de la compuerta AND vista anteriormente.
Esto modifica su tabla de verdad, de hecho la invierte (se dice que la niega) quedando que la salida solo será un 0 cuando todas sus entradas estén en 1.
El pequeño círculo en su salida es el que simboliza la negación. El numero de entradas debe ser como mínimo de dos, pero no es raro encontrar NAND de 3 o mas entradas.
ENTRADA A ENTRADA B SALIDA X
0 0 1
0 1 1
1 0 1
1 1 0
COMPUERTA NOR (NO O)
De forma similar a lo explicado con la compuerta NAND, una compuerta NOR es la negación de una compuerta OR, obtenida agregando una etapa NOT en su salida.
Como
podemos ver en su tabla de verdad, la salida de una compuerta NOR es 1
solamente cuando todas sus entradas son 0. Igual que en casos
anteriores, la negación se expresa en los esquemas mediante un círculo
en la salida. El número de entradas también puede ser mayor a dos.
ENTRADA A ENTRADA B SALIDA X
0 0 1
0 1 0
1 0 0
1 1 0
COMPUERTA XOR (O Exclusivo)
La
compuerta OR vista anteriormente realiza la operación lógica
correspondiente al O inclusivo, es decir, una o ambas de las entradas
deben estar en 1 para que la salida sea 1.
Un ejemplo de esta compuerta en lenguaje coloquial seria “Mañana iré de compras
o al cine”. Basta con que vaya de compras o al cine para que la
afirmación sea verdadera. En caso de que realice ambas cosas, la
afirmación también es verdadera. Aquí es donde la función XOR difiere de
la OR: en una compuerta XOR la salida será 0 siempre que las entradas
sean distintas entre si. En el ejemplo anterior, si se tratase de la
operación XOR, la salida seria 1 solamente si fuimos de compras o si
fuimos al cine, pero 0 si no fuimos a ninguno de esos lugares, o si
fuimos a ambos.
Esta característica hace de la compuerta XOR un componente imprescindible en los circuitos sumadores de números binarios, tal como los utilizados en las calculadoras electrónicas.
ENTRADA A ENTRADA B SALIDA X
0 0 0
0 1 1
1 0 1
1 1 0
COMPUERTA NXOR (NO O EXCLUSIVO)
No
hay mucho para decir de esta compuerta. Como se puede deducir de los
casos anteriores, una compuerta NXOR no es más que una XOR con su salida
negada, por lo que su salida estará en estado alto solamente cuando sus
entradas son iguales, y en estado bajo para las demás combinaciones
posibles.
ENTRADA A ENTRADA B SALIDA X
0 0 1
1 0 0
0 1 0
1 1 1
Tras la invención del transistor, con la invención del
circuito integrado
se abrió el camino hacia lo que prometió ser una miniturización aún más
dramática de componentes electrónicos que prometía reducir enormemente
el espacio ocupado por cualquier aparato electrónico, reducir
enormemente el consumo de energía para poder tenerlo operando, y reducir
el costo de los componentes usados para construir un equipo
electrónico. Es así como empezaron a surgir diseños óptimos que por su
simpleza y bajo costo comenzaron a utilizarse como "ladrillos" básicos
para la integración a gran escala que estaba por llegar. Las familias
lógicas de circuitos integrados en un principio fueron identificadas
casi todas ellas por tres letras como RTL, TTL, DTL, MOS; o por cuatro
letras como DCTL y CMOS, una costumbre que todavía prevalece hasta
nuestros días. A continuación tenemos un resumen de lo que hay detrás de
estos acrónimos.
La lógica DTL (Diode-Transistor-Logic)
Aquí el diseño básico está centralizado en torno a un transistor bipolar
en cuya entrada se han añadido varios diodos, como lo muestra el
siguiente diagrama esquemático:
La forma en la que trabaja este circuito es la siguiente: supóngase que todas las tres entradas
A,
B y
C están conectadas al nivel de voltaje alto (en este caso,
Vcc),
que identificaremos aquí de la manera usual como un "1" lógico. Siendo
así, habrá una señal de entrada en la base del transistor que ocasionará
que dicho transistor conduzca corriente eléctrica, lo cual hará que la
salida del transistor caiga prácticamente al nivel de "0". Ahora bien,
si cualquiera de las tres entradas
A,
B y
C recibe
una señal de "0", o sea si cualquiera de los diodos a la entrada es
"aterrizado" a tierra eléctrica con una señal de "cero", el voltaje a la
entrada de la base del transistor será prácticamente de cero, con lo
cual el transistor no conducirá corriente eléctrica alguna y por lo
tanto el voltaje de salida del mismo será igual a
Vcc o a "1". Este comportamiento lo podemos resumir de la manera siguiente: si cualquiera de las entradas
A,
B ó
C
toma un valor de "0", la salida será "1". Unicamente cuando todas las
entradas tienen un valor de "0" podremos tener una salida de "0". Si
recordamos bien lo que vimos en los capítulos anteriores, esta es
precisamente la función NAND, como lo indica la función Boleana puesta a
la derecha a la salida del colector del transistor. Es así como el
bloque fundamental de la lógica DTL viene siendo precisamente la función
NAND.
La lógica DCTL (Direct-Coupled Transistor Logic)
A diferencia del diseño anterior que requiere un diodo para implementar
cada entrada, la lógica DCTL requiere del uso de un transistor para
implementar cada entrada de la compuerta lógica, lo cual naturalmente
aumenta el costo y la complejidad del circuito. El diagrama esquemático
para el componente esencial de esta clase de lógica es el siguiente:
La forma en la cual trabaja este circuito es la siguiente: supóngase que ambas entradas
A y
B
no están recibiendo voltaje alguno, estando ambas conectadas a "tierra
eléctrica" (que viene siendo el equivalente de una señal de "cero"). En
tal caso, ninguno de los dos transistores estará conduciendo corriente
eléctrica alguna, y la salida será igual al voltaje
Vcc,
o sea un "1" lógico. Si aplicamos un voltaje a cualquiera de los dos
transistores (o sea una señal de "1") o a ambos, entonces la salida
unida de ambos colectores caerá a un voltaje prácticamente de cero.
Puesto de otra manera, si cualquiera de las dos entradas
A y/o
B
toma un valor de "uno", la salida caerá a "cero". Se requiere que ambas
entradas sean "0" para que la salida sea "1". Esta es precisamente la
función lógica NOR, como lo indica la expresión Boleana puesta a la
derecha a la salida conjunta de los colectores de ambos transistores.
La lógica RTL (Resistor-Transistor-Logic)
Esta clase de circuitos integrados fue la primera que proporcionó en el
mercado componentes lógicos discretos a bajo costo con los cuales se
empezaron a implementar muchas funciones lógicas básicas. Aunque todavía
no había alguna "estandarización" llevada a cabo por las empresas que
iniciaron la fabricación de circuitos integrados RTL, por vez primera se
empezaron a fabricar muchos tipos de circuitos que además de funciones
lógicas básicas implementaban algunas funciones algo más sofisticadas,
como contadores binarios o registros de transferencia.
Por la forma en la cual está integrada la electrónica interna, el
"bloque fundamental" de la familia RTL no es ninguna de nuestras
funciones lógicas básicas (OR, AND, NOT), sino la función NOR. El bloque
NOR es el "caballito de batalla" de la familia RTL.
Los circuitos integrados RTL siempre se destacaron por ser una familia
de componentes muy resistentes a cualquier tipo de falla. Inclusive en
la literatura promocional de los mismos se afirmaba que no había forma
posible de dañarlos aunque al construír un prototipo usando circuitos
RTL se cometiesen errores al hacer las conexiones eléctricas. Quizá uno
de los libros que más contribuyeron a popularizar el uso de los
circuitos integrados de la familia RTL fue el libro "RTL Cookbook" de
Don Lancaster, un personaje tan pintoresco como prolífico que tuvo la
virtud de hacer accesibles en sus libros conocimientos que anteriormente
sólo estaban al alcance de estudiantes de la carrera de ingeniería
eléctrica en universidades de prestigio.
Entre algunos de los circuitos integrados construídos con tecnología RTL
podemos mencionar como ejemplos los siguientes, construídos por la
empresa Motorola:
MC789P -- Hex inverter (seis inversores NOT)
MC724P -- Quad two input gate (cuatro NORs de dos entradas)
MC790P -- Dual J-K Flip-Flop (dos flip-flops J-K)
Además de estos componentes podemos mencionar el
ul914 (
Dual two input NOR, dos NOR de dos entradas) construido por varios fabricantes.
Para quienes tienen nociones básicas de electrónica elemental, a
continuación se reproduce el diagrama esquemático que muestra la manera
en la cual opera un circuito RTL esencial, un NOR de tres entradas
A,
B y
C, en cuya construcción se utilizan tres transistores y cuatro resistencias:
La forma en la que trabaja este circuito es la siguiente: cuando las
tres entradas están "aterrizadas a tierra" (el símbolo que aparece en la
parte más inferior del diagrama), lo cual equivale a un cero (0)
lógico, los tres transistores permanecen desactivados, no conducen
ninguna corriente, con lo cual a la salida de los mismos será igual al
voltaje Vcc que equivale al uno (1) lógico. En otras palabras, cuando
todas las entradas son (0), la salida es (1). Pero cuando una de las
entradas
A,
B o
C
recibe un voltaje, un (1), entonces el transistor al cual le llega la
señal empieza a conducir, con lo cual se desploma el voltaje de salida.
En otras palabras, si cualquiera de las entradas tiene un valor de (1),
la salida caerá a (0). La salida será (1) únicamente cuando todas las
entradas sean (0). Esta es precisamente la función NOR.
La familia RTL quedó descontinuada del mercado cuando hizo su aparición
una nueva familia de circuitos integrados basada en otra tecnología que
veremos a continuación.
TECNOLOGÍA TTL
Aquí podemos hablar ya de toda una verdadera familia
de circuitos lógicos basada en la tecnología TTL, la cual fue creada
por la compañía Texas Instruments (la misma compañía que dió el primer
impulso fuerte al desarrollo de los circuitos con un nivel elevado de
integración).
El circuito integrado básico de esta familia es el 7400,
también identificado en mucha literatura técnica como el SN7400, aunque
en realidad las siglas SN puestas al principio simplemente identifican
de modo único a la compañía Texas Instruments, el fabricante que dió
inicio a esta primera gran familia de circuitos integrados
(supuestamente en un principio las siglas simplemente significaban
"número de serie" o Serial Number,
perdiéndose este significado inicial con el paso del tiempo). El
"diagrama esquemático" y el aspecto físico de este circuito integrado en
su presentación como paquete DIP (dual in-line package) se muestran a continuación (el símbolo "&", conocido como el ampersand
y el cual se lee en inglés precisamente como "and", puesto dentro de
cada bloque lógico, en conjunción con la burbuja inversora se debe leer
en estos diagramas esquemáticos como "nand"):

La siguiente figura muestra cómo está montada dentro de estos encapsulamientos de plástico DIP la "pastilla de silicón" o wafer:

Aunque la familia TTL en cierta forma ya está algo obsoleta, superada
por las familias CMOS, los circuitos integrados TTL fueron tan
utilizados que aún hay muchos de ellos en operación.
LA FAMILIA SCHOTTKY TTL
Un paso posterior en la evolución de la familia TTL fue la
implementación en los circuitos integrados de la misma de diodos basados
en el diodo Schottky, el cual es representado en los diagramas esquemáticos con el siguiente símbolo:
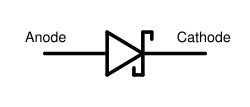
Permitió incrementar de forma considerable la rapidez con la cual los
circuitos integrados podían llevar a cabo sus operaciones. La
identificación de un circuito integrado de la familia Schottky TTL es la
misma que la utilizada por la familia TTL, excepto que para denotar su
mayor velocidad se le agrega una "S" intermedia a la nomenclatura de
cada componente de la familia. De este modo, el equivalente pin-por-pin del circuito integrado 7400 vendría siendo el circuito integrado 74S00,
que a su vez vendría siendo el bloque fundamental de esta familia. La
nomenclatura se mantiene constante a través de todos los componentes de
esta familia. Por ejemplo, en el circuito integrado 74S32, los primeros
dos dígitos "74" indican que es un circuito integrado correspondiente a
la familia TTL, los últimos dos dígitos "32" indican que se trata de un
paquete que incluye cuatro compuertas OR de dos entradas cada una, y la
letra "S" intermedia indica que se trata de un circuito integrado de
alta velocidad.
LA FAMILIA CMOS
Así como Texas Instruments se convirtió en una empresa pionera al
introducir la familia lógica basada en la tecnología TTL, también la
empresa RCA llevó a cabo el siguiente proceso evolutivo introduciendo
como una alternativa a la familia TTL una serie de circuitos integrados
basados en una tecnología que requiere un consumo muy bajo de energía:
la familia CMOS (Complementary Metal-Oxide-Semiconductor). El acrónimo
indica que para la construcción de estos circuitos se utiliza ya no el
transistor bipolar sino el transistor MOS basado a su vez en el
transistor de efecto de campo (field effect transistor),
apareado en pares de modo tal que puedan implementar una de varias
compuertas lógicas de las maneras que veremos a continuación. La gran
ventaja de este tipo de componentes es que presentan una alta impedancia
(resistencia eléctrica) de entrada consumiendo por lo tanto muy poca
corriente eléctrica. El bajo consumo de corriente eléctrica hace a esta
tecnología atractiva en aplicaciones en las cuales es imperativo el
ahorro de energía (principalmente artículos electrónicos operados con
batería portátil desechable). Sin embargo, su velocidad es inferior a la
velocidad de la familia TTL, de modo tal que cada familia tiene aquí
sus pros y sus contras.
Por la forma en la cual está integrada la electrónica interna, el
"bloque fundamental" de la familia CMOS no es tampoco ninguna de
nuestras funciones lógicas básicas (OR, AND, NOT), sino, al igual que en
el caso de la familia RTL, puede ser ya sea la función NOR o también la
función NAND. El circuito integrado básico de la gran familia
progenitora de las compuertas lógicas CMOS es el 4000, basado en los bloques NOR, cuya relación de pins es la siguiente:
A continuación tenemos el "diagrama esquemático" de los pines proporcionados por otros de los circuitos lógicos pertenecientes a esta
familia:
La tecnología CMOS se ha vuelto tan importante, que no podemos cerrar
este Suplemento sin dar una idea así sea generalizada sobre cómo trabaja
la electrónica CMOS, para beneficio de los lectores que tengan algunas
nociones elementales sobre cuestiones eléctricas.